tree

前言对二叉树有一定了解之后，学习一下对二叉树的操作，有时候这些东西一学就忘，反复操作几回就熟了。二叉树的概念已经了解了，那么得知道怎么操作。现在就讲讲怎么操作二叉树。 构建二叉树首先得先种一颗树，然后才能操作树。怎么构建？有哪些对象、需要什么方法？ 主要对象 Node 节点对象 BinaryTree 树对象 Node 节点对象作用：存数据的。大白话就是树中的每一个节点，存着外面进来的数据。最简单的理解就是HashMap就是一颗树的实现，每次不明白，就想想HashMap，是不是就通了。 四个关键要素： left right key value BinaryTree 对象作用：操作node节点数据，维护树结构。大白话，就是把Node拼起来，成为一颗大树。主要操作： put get delete size min max put 完以后要返回整棵树，开始是始于 root，返回也是返回 root。 实现实现就是把Node和BinaryTree这两结合起来用，还用的没问题。需要考虑几个问题： 怎么结合起来用 从哪开始写 怎么结合起来用？即然要操作，那就需要对外暴露操作接口Binar ...

概念前面对树已经有了一个认识，现在看下红黑树的定义。开始之前提几个问题： 什么是红黑树 有什么用 怎么实现 优缺点 什么是红黑树红黑树: 又叫二叉平衡树红黑树又红又黑，真正的意义是什么？为什么要红一下黑一下？ 会左旋 和 右旋，不会出现单边增长太多，会平衡。 红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的：它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。 有什么用 为了实现快速定位而设计的算法。 几乎所有基于二叉树的算法，都是基于二分法进行查找的，只要数据100%是按照一定顺序排列的，那么就可以被二分法查找。 假疫有10亿数据只需要不到30次比较就能查找到目标。 二叉查找树这一数据结构并不难，而红黑树之所以难是难在它是自平衡的二叉查找树，在进行插入和删除等可能会破坏树的平衡的操作时，需要重新自处理达到平衡状态。 红黑树特点： 节点要么红、要么黑 根节点是黑色 叶节点null，都是黑色 每个红色节点 ...

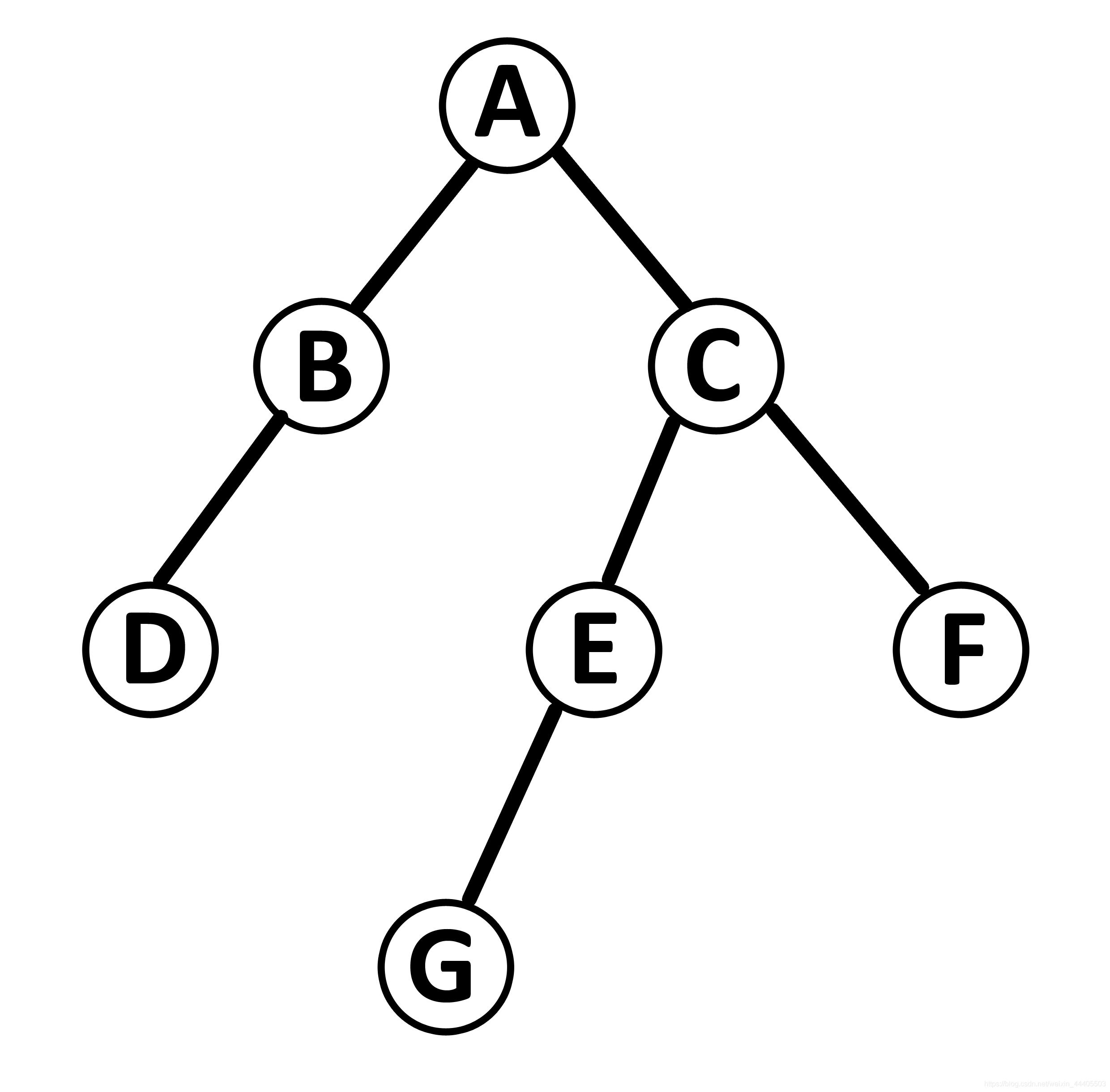
树即经典实用，又非常有助于学习算法。 前言二叉树是一个经典的数据结构，通过学习二叉树可以往后扩展学习更多类型的树。这里要强调几点： 树是逻辑上定义的数据结构，哪怕只有一个节点也可以称之为树。 不要慌，二叉树实际上比你想像的要容易上手。 这篇文章先讲概念，再讲实现。 二叉树二叉查找树也称为有序二叉查找树，满足二叉查找树的一般性质，是指一棵空树具有如下性质： 任意节点左子树不为空,则左子树的值均小于根节点的值； 任意节点右子树不为空,则右子树的值均大于于根节点的值； 任意节点的左右子树也分别是二叉查找树； 没有键值相等的节点； 不区分左右节点的值谁比谁大。叶子节点：没有子节点的节点。由于出版的问题，节点 和 结点 是一个意思。 二叉树五种状态树的五种状态要这样理解：为了抽象出树的各种情况下树当时的状态，而进行的命名。实际上就是当前树被操作当前状态。 空树: 就是null，一般是在操作中删完了。 单节点树：只有一个根结点的二叉树 只有左子树 只有右子树 满二叉树：每一次结构都达到最大值。就是完美状态总节点数=2^n-1，n 为层数。(等比数列求和) 完全二权树：叶子节点只能出 ...

前言 树是一种逻辑上的概念，切记，这会帮助你理解。 学习算法过程中你不得立即获得正向反馈，这就是学习无奈的地方，学习更像是一种投资。不要觉得学习带有功利性不好，努力考上一个好大学，找到好工作也是一种功利性，只是平时不愿意承认。学习算法也是，你可以找到好工作，这是一种长期投资。坚持下去。 树 树是一种逻辑上的概念，切记，这会帮助你理解。 树是一种数据结构它是由n（n>=1）个有限结点组成一个具有层次关系的集合。即最少一个节点。 树具有的特点有 每个结点有零个或多个子结点 没有父节点的结点称为根节点 每一个非根结点有且只有一个父节点 除了根结点外，每个子结点可以分为多个不相交的子树。 术语 结点的度(Degree)：结点拥有的子树的数目，root，有 0-2个结点 叶子结点：度为0的结点 //就是最后一个节点 分支结点：度不为0的结点 树的度：树内各结点的度的最大的值。（即所有子节点加起来有多少度） 树的层次序号：每个节点，从上往下，从左往右都有一个编号，根是1，第二层最左是2依次递进 层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1 树的 ...