算法二叉树的构建和查找

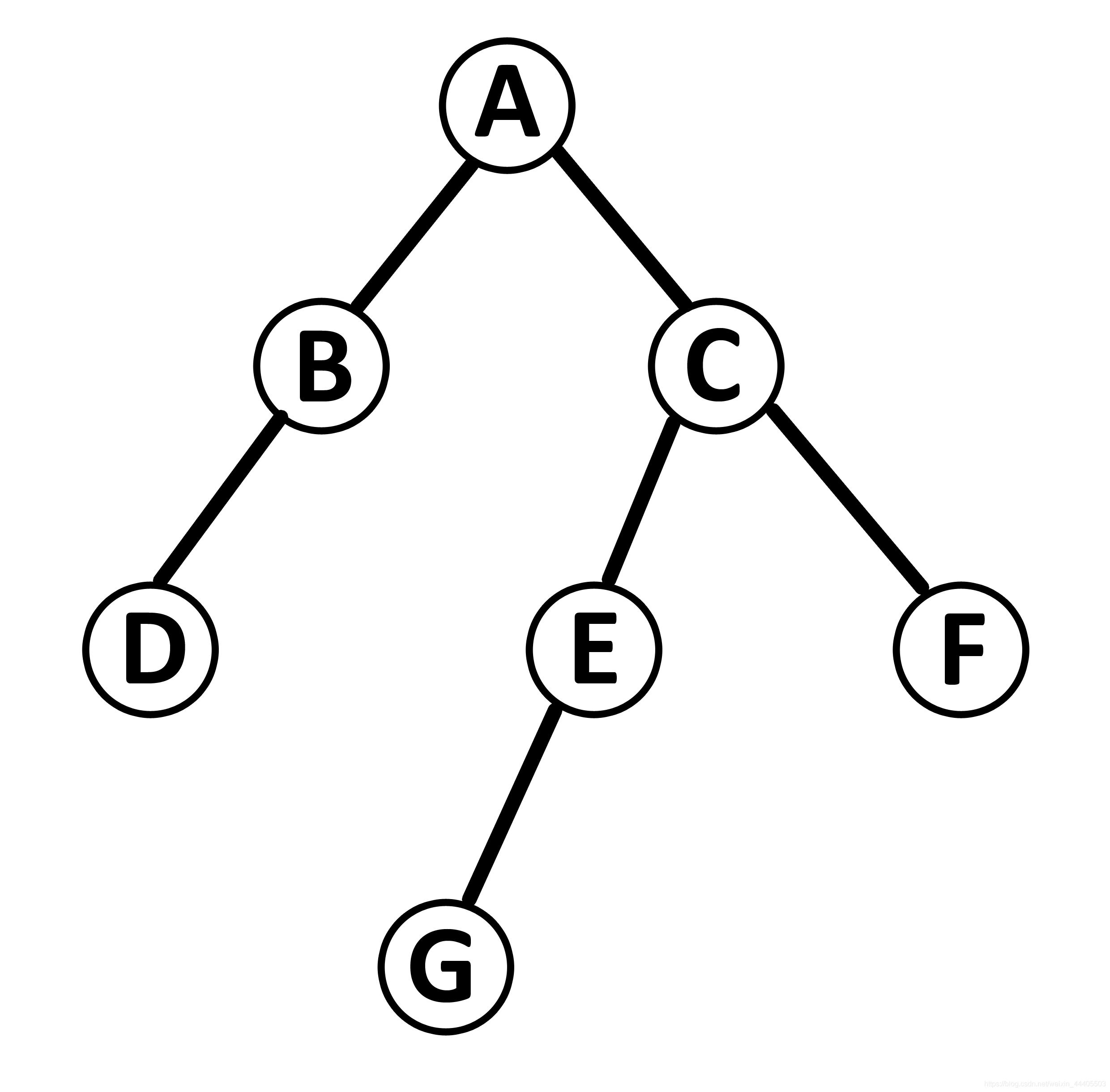
前言

对二叉树有一定了解之后，学习一下对二叉树的操作，有时候这些东西一学就忘，反复操作几回就熟了。
二叉树的概念已经了解了，那么得知道怎么操作。现在就讲讲怎么操作二叉树。

构建二叉树

首先得先种一颗树，然后才能操作树。
怎么构建？有哪些对象、需要什么方法？

主要对象

Node 节点对象
BinaryTree 树对象

Node 节点对象

作用：存数据的。
大白话就是树中的每一个节点，存着外面进来的数据。最简单的理解就是HashMap就是一颗树的实现，每次不明白，就想想HashMap，是不是就通了。

四个关键要素：

left
right
key
value

BinaryTree 对象

作用：操作node节点数据，维护树结构。
大白话，就是把Node拼起来，成为一颗大树。
主要操作：

put
get
delete
size
min
max

put 完以后要返回整棵树，开始是始于 root，返回也是返回 root。

实现

实现就是把Node和BinaryTree这两结合起来用，还用的没问题。
需要考虑几个问题：

怎么结合起来用
从哪开始写

怎么结合起来用？
即然要操作，那就需要对外暴露操作接口BinaryTree就是最外操作的对象。

从哪开始写？
先定义数据结构，再定义方法。

查询和添加逻辑基本相同，都是通过递归的形式。
删除比较麻烦，如果被删除的节点有子节点，不能让丢掉这些子节点，需要重新维护这些子节点。
删除的节点，左子树的所有节点一定比右子树的节点小，所以只需要从右子树中拿到最小的那个节点即可，也就是右子树中最左边的叶子节点。

删除步骤

找到要删除的 key
判断如果左子树为空，就用右边最小
判断如果右子树为空，就用左边最小
删除找到的最小值
将最小值替换被删除的节点，重新跟左右子节点建立连接
简化的情况
被删除节点只有一个左子树或右子树，直接拿过来替换当前节点就行

实现代码：

import java.util.Queue;
import java.util.concurrent.ArrayBlockingQueue;

/**
 * 二叉树
 * 左小右大
 *
 * @author liu kai
 * @since 2015/5/30 19:30.
 */
public class BinaryTree<Key extends Comparable<Key>, Value> {

  //根节点
  private Node root;
  //个数
  private int size;

  private class Node {
    public Node left;
    public Node right;
    public Key key;
    public Value value;

    public Node(Key key, Value value, Node left, Node right) {
      this.left = left;
      this.right = right;
      this.key = key;
      this.value = value;
    }
  }

  public void put(Key key, Value value) {
    root = put(root, key, value);
  }

  // 插入
  private Node put(Node x, Key key, Value value) {
    if (x == null) {
      size++;
      return new Node(key, value, null, null);
    }
    int comp = key.compareTo(x.key);
    // key 比当前节点小，往左
    if (comp > 0) {
      x.right = put(x.right, key, value);
      // key 比当前节点大，往右
    } else if (comp < 0) {
      x.left = put(x.left, key, value);
      // 相等，就是当前节点，替换值
    } else {
      x.value = value;
    }
    return x;
  }

  // 查询
  public Value get(Key key) {
    return get(root, key);
  }

  private Value get(Node x, Key key) {
    if (x == null) {
      return null;
    }

    int comp = key.compareTo(x.key);
    // key 比当前节点小，往左
    if (comp > 0) {
      return get(x.right, key);
      // key 比当前节点大，往右
    } else if (comp < 0) {
      return get(x.left, key);
      // 相等，就是当前节点，替换值
    } else {
      return x.value;
    }
  }

  public int size() {
    return size;
  }

  public Node delete(Key key) {
    return delete(root, key);
  }

  // x 当前要被删除的点节
  private Node delete(Node x, Key key) {
    if (x == null) {
      return null;
    }
    int comp = key.compareTo(x.key);
    //   1 张三
    //   /   \
    // 2李四  3王五
    //         \
    //        4工作
    if (comp > 0) {
      x.right = delete(x.right, key);
    } else if (comp < 0) {
      x. left = delete(x.left, key);
    } else {

      //1.简单情况：
      // 被删除节点只有一个 左子树 或 右子树，直接拿过来替换当前节点就行
      if (x.left == null) {
        size--;
        return x.right;
      }
      if (x.right == null) {
        size--;
        return x.left;
      }
      size--;
      Node minNode = x.right;
      //2.找到最左节点
      while (minNode.left != null) {
        // 如果 minNode 没有子节点了，说明 minNode 是最小节点
        // 这里 minNode 是当前节点， .left 就是它的子节点
        minNode = minNode.left;
      }

      // 3.断开最左节点和上个节点的联系
      // 由于没有记录父节点是谁，所以需要再次遍历
      Node parent = x.right;
      while (parent.left != null) {
        // 当前节点的子节点没有子节点，就是最小节点
        if (parent.left.left != null) {
          parent.left = null;
        } else {
          parent = parent.left;
        }
      }

      // 4.建立连接
      // 再跟左右子树建立连接，再跟父节点建立连接
      minNode.left = x.left;
      minNode.right = x.right;

      return x;
    }
    return x;
  }
}