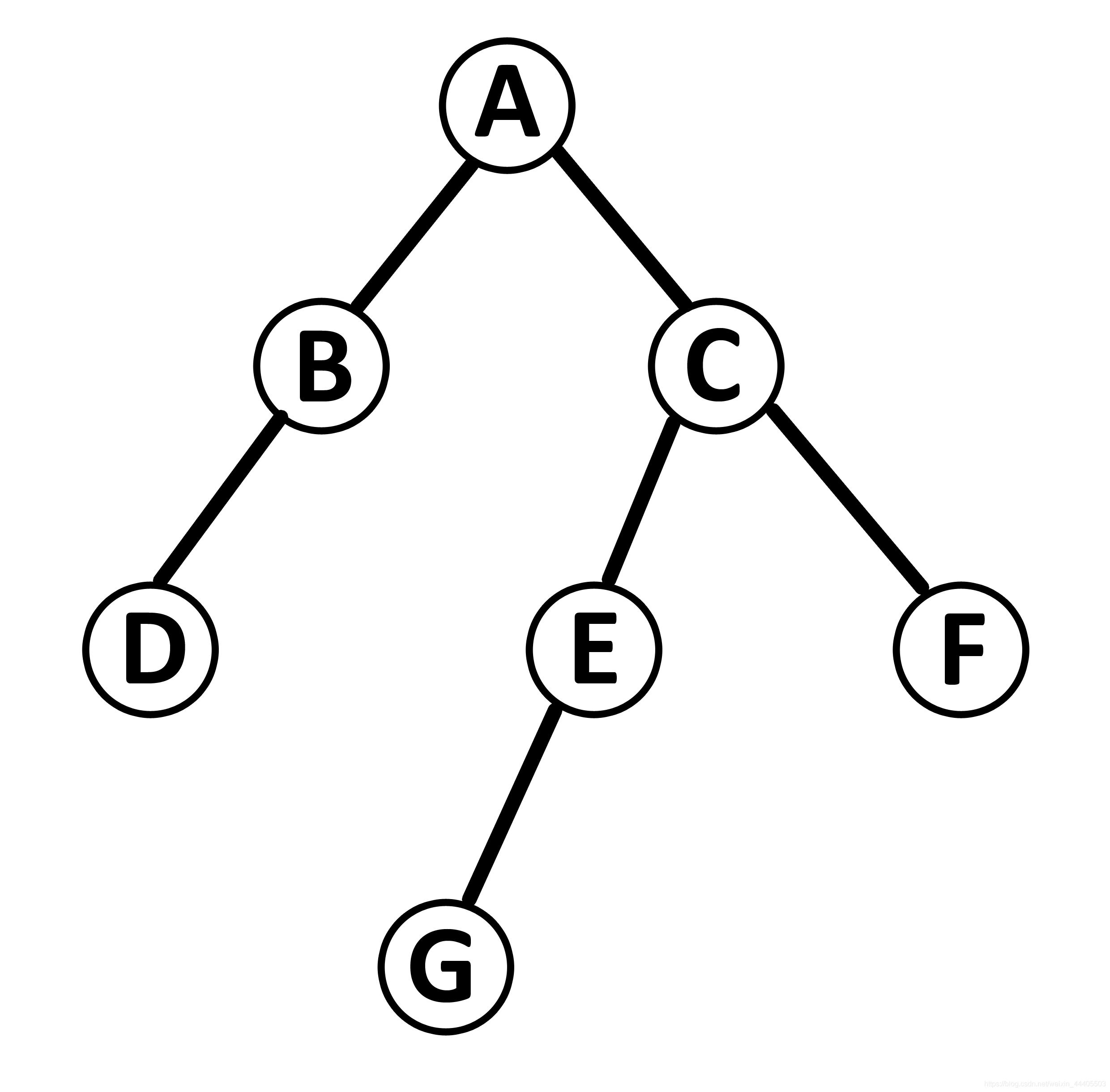
算法--二叉树

树即经典实用，又非常有助于学习算法。

前言

二叉树是一个经典的数据结构，通过学习二叉树可以往后扩展学习更多类型的树。
这里要强调几点：

1. 树是逻辑上定义的数据结构，哪怕只有一个节点也可以称之为树。
2. 不要慌，二叉树实际上比你想像的要容易上手。

这篇文章先讲概念，再讲实现。

二叉树

二叉查找树也称为有序二叉查找树，满足二叉查找树的一般性质，是指一棵空树具有如下性质：

1. 任意节点左子树不为空,则左子树的值均小于根节点的值；
2. 任意节点右子树不为空,则右子树的值均大于于根节点的值；
3. 任意节点的左右子树也分别是二叉查找树；
4. 没有键值相等的节点；

不区分左右节点的值谁比谁大。
叶子节点：没有子节点的节点。
由于出版的问题，节点 和 结点 是一个意思。

二叉树五种状态

树的五种状态要这样理解：为了抽象出树的各种情况下树当时的状态，而进行的命名。实际上就是当前树被操作当前状态。

1. 空树: 就是null，一般是在操作中删完了。
2. 单节点树：只有一个根结点的二叉树
3. 只有左子树
4. 只有右子树
5. 满二叉树：每一次结构都达到最大值。就是完美状态
   总节点数=2^n-1，n 为层数。(等比数列求和)
6. 完全二权树：叶子节点只能出现在最下层 和 次下层

形态展示

形态一 空树

(null)

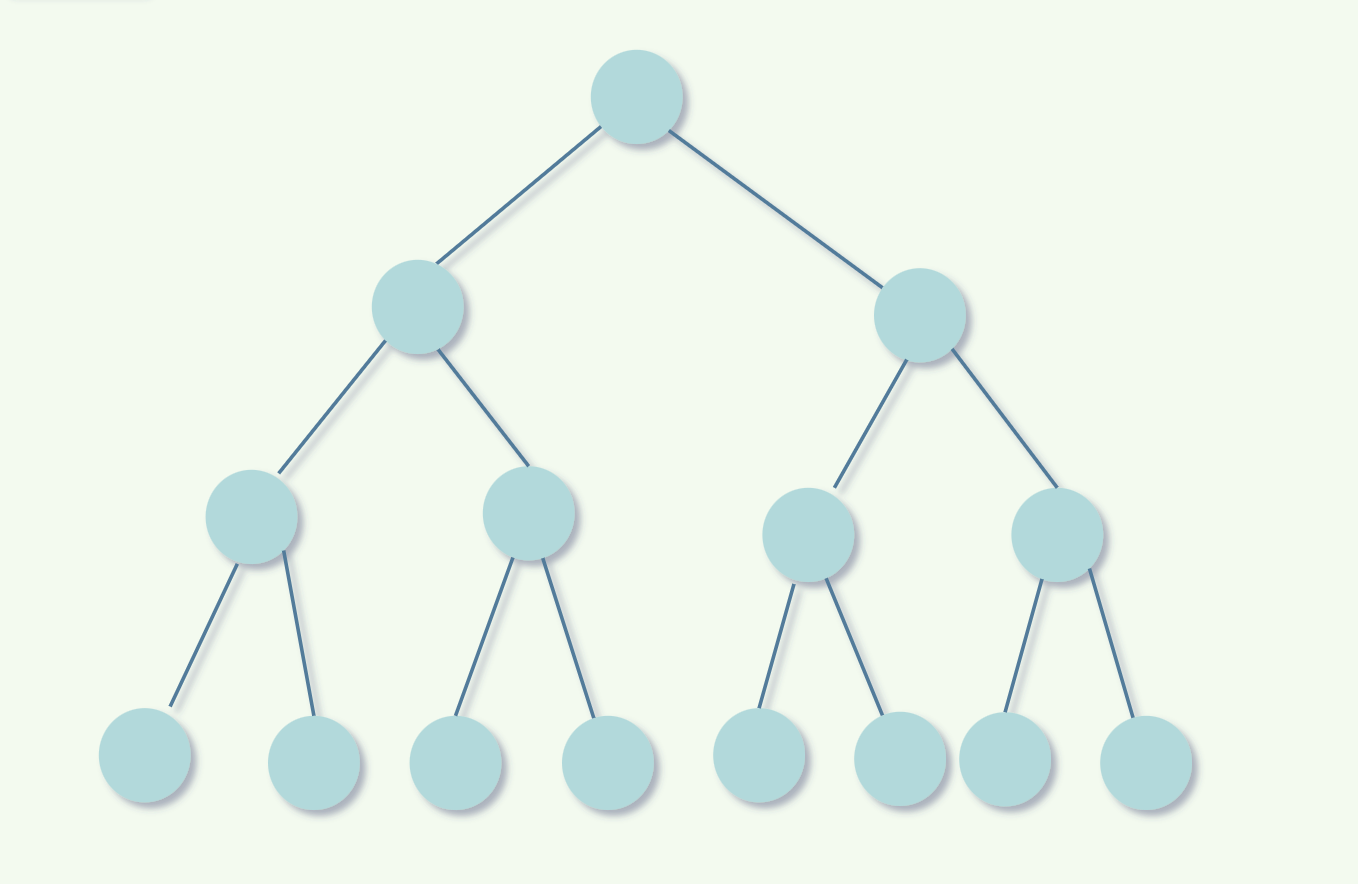
形态二: 满二叉树

只有叶子节点多一个少一个就不是完全二叉树

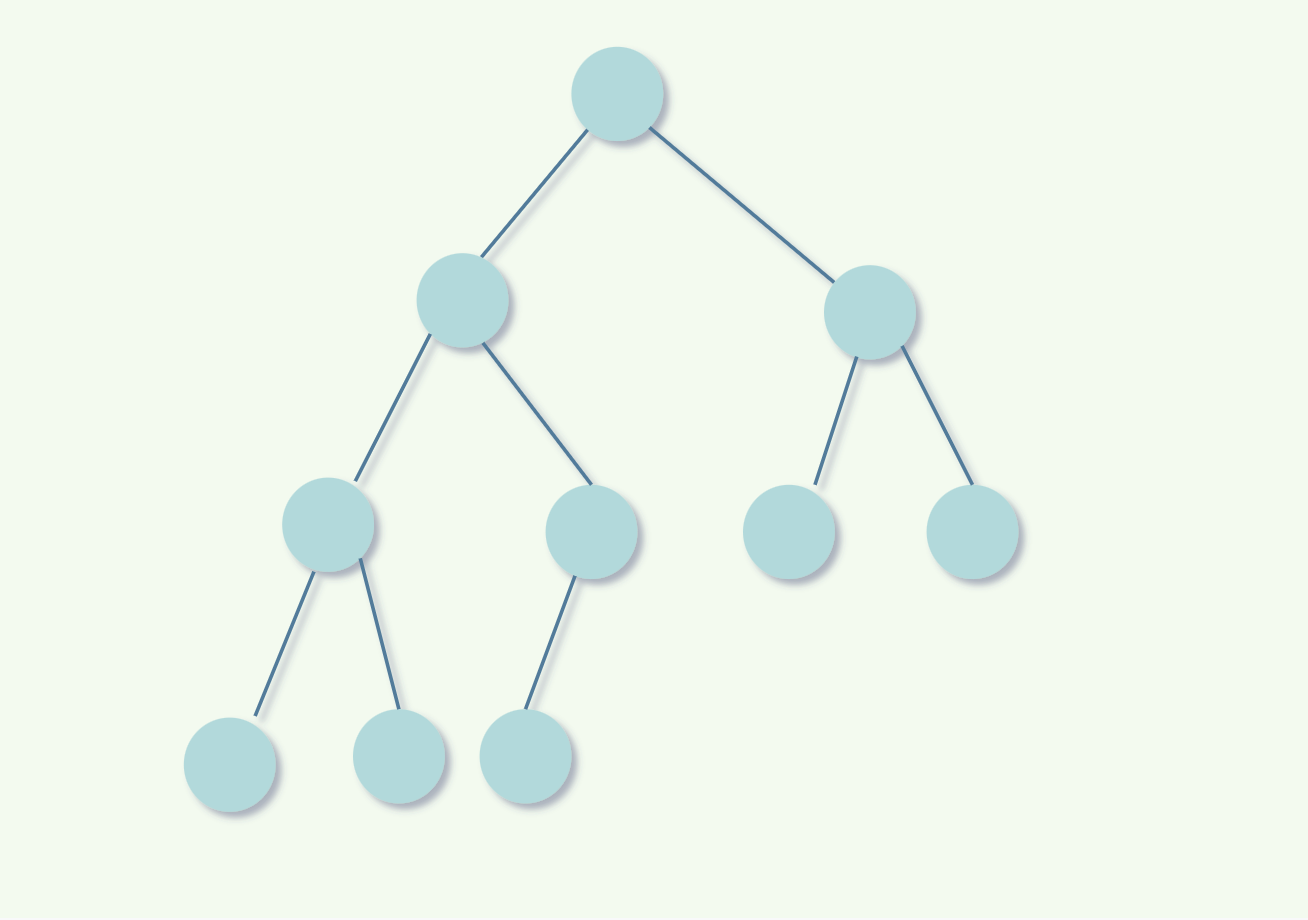
形态三：完全二叉树

定义：左满，右不满，叶子节点只能出现在最下层 和 次下层

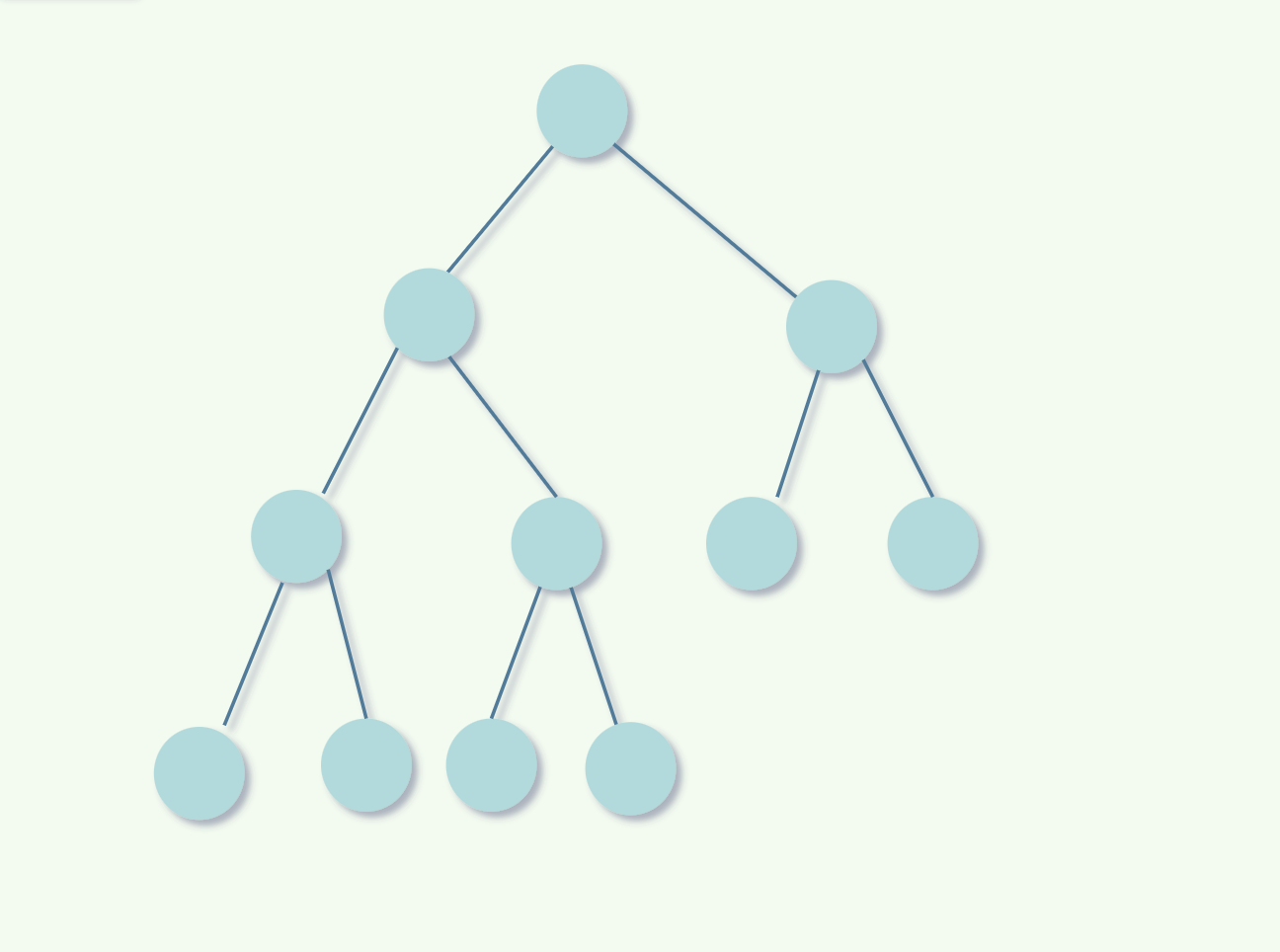
这也是完全二叉树，左满又不满。

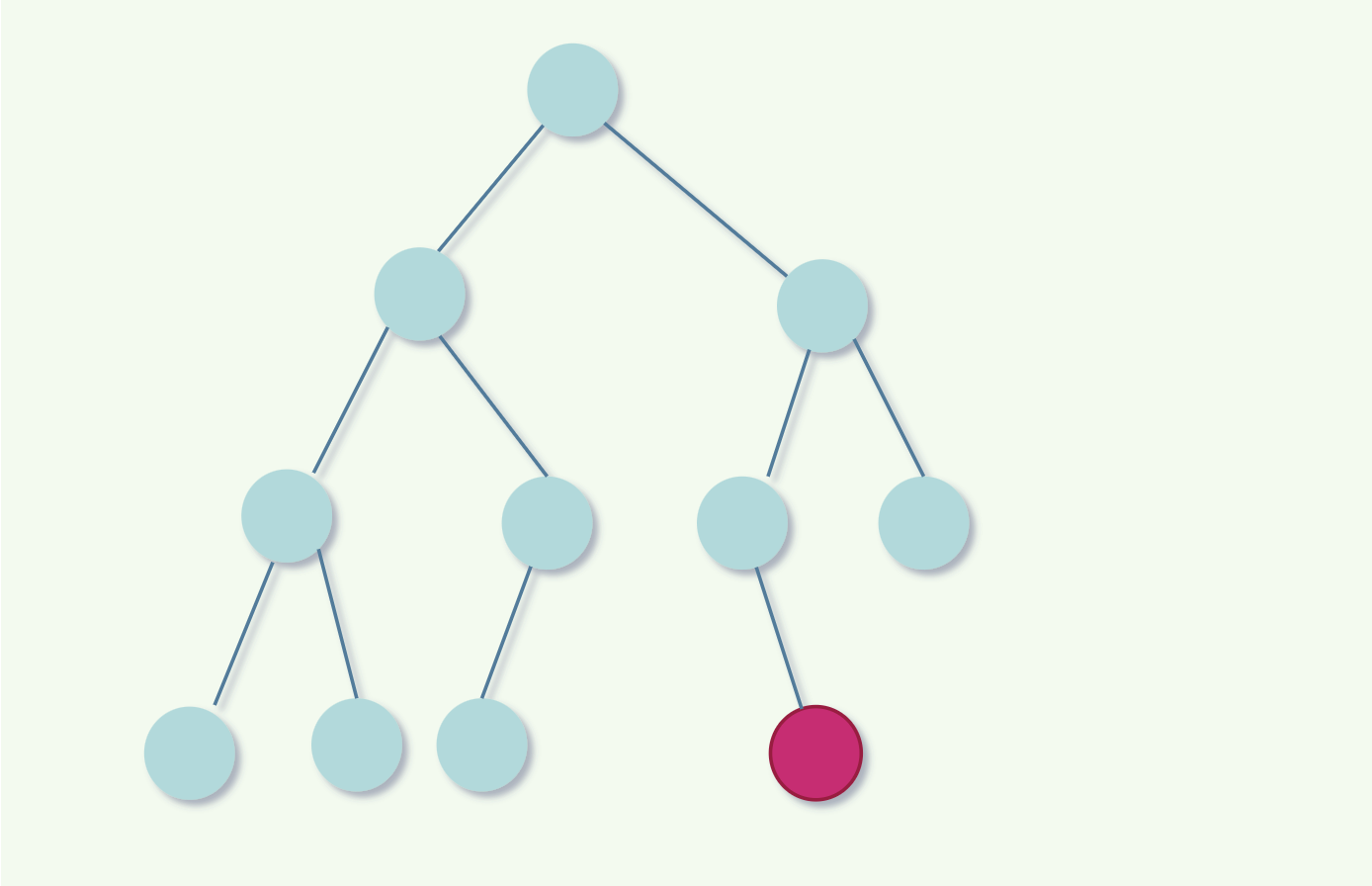
这种就不是完全二叉树，酒红色节点在右边，所以不满足最左原则。

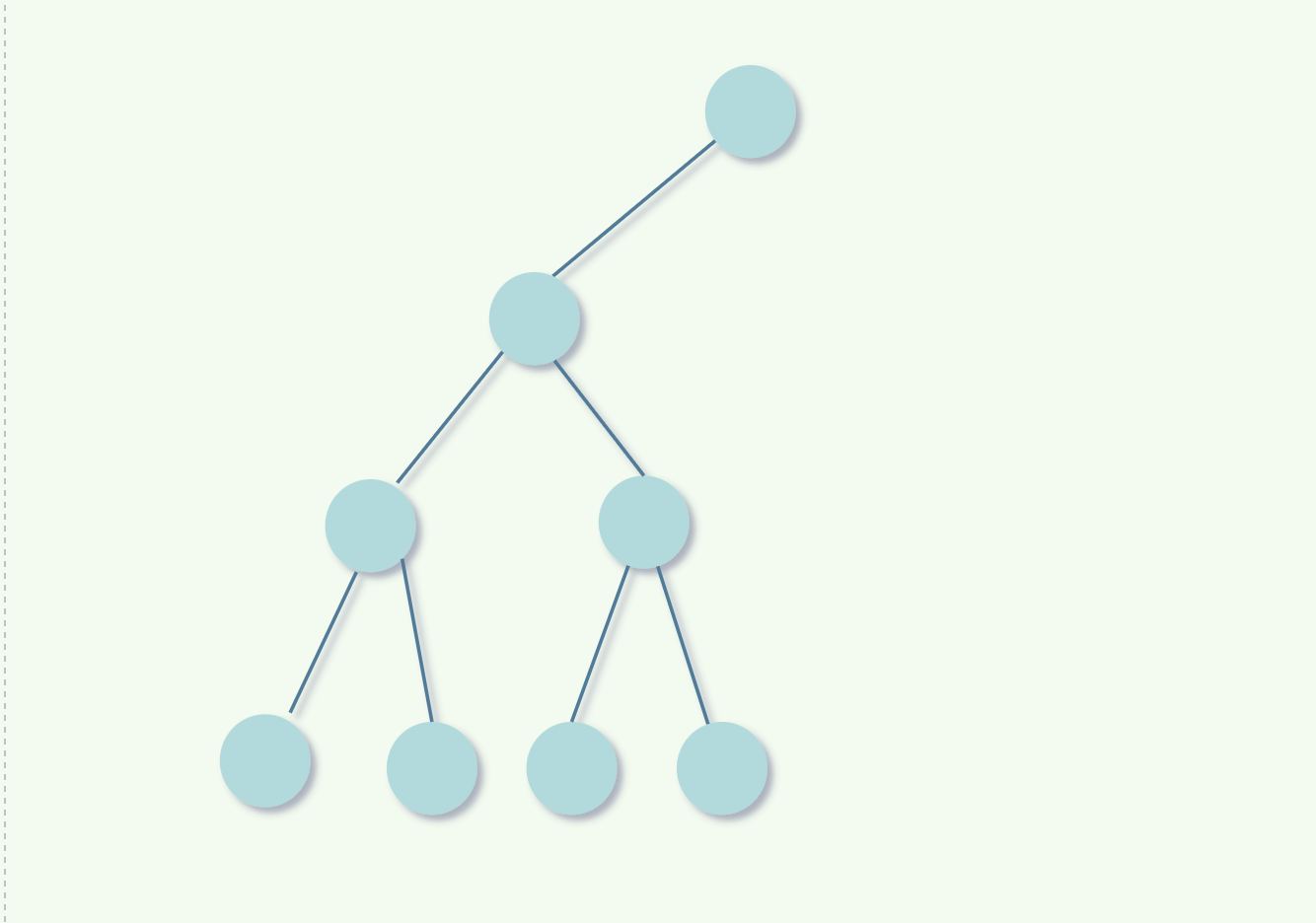
形态四 左子树

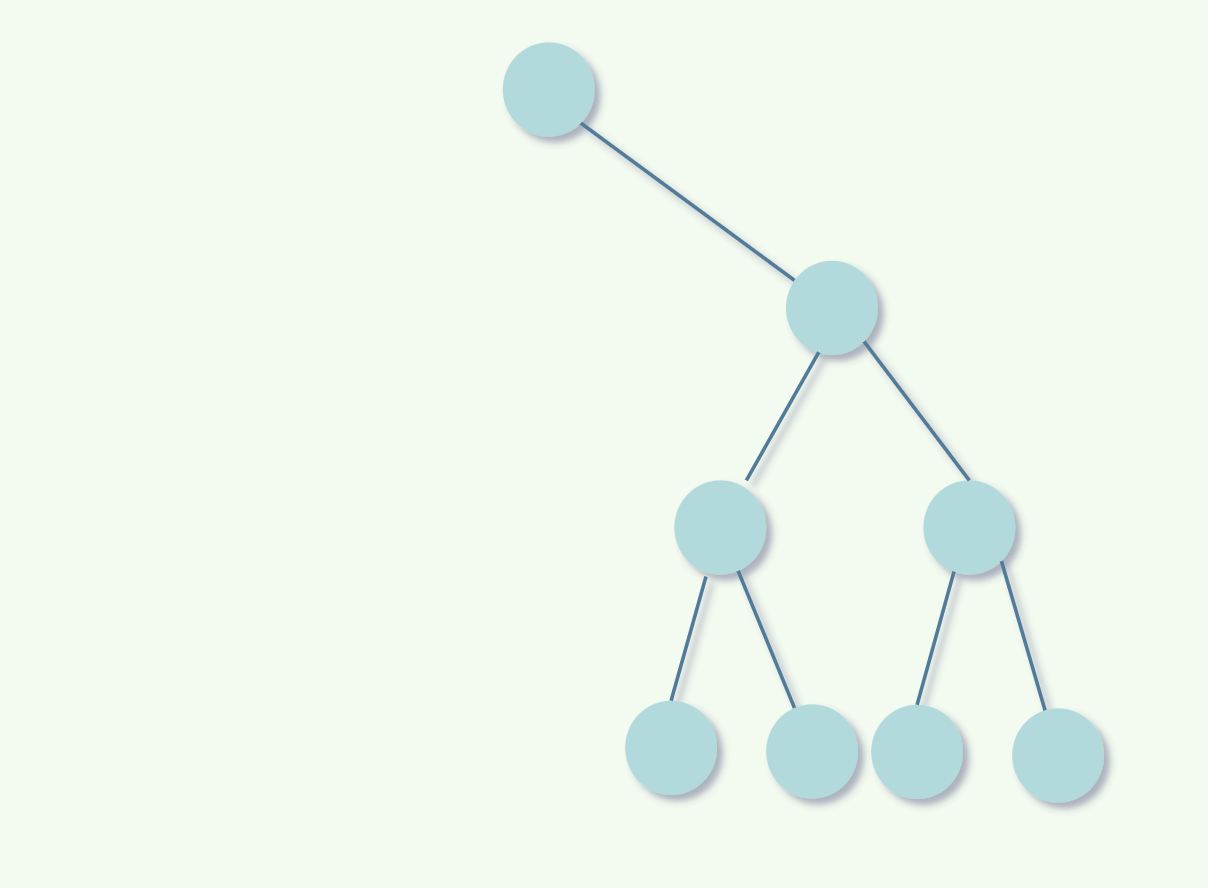
形态五 右子树

遍历二叉树

二叉树遍历 - 前序、中序、后序：时间复杂度是多少？
前序：先输出父节点
中序：先输出左子树，再输出父节点，右子树
后序：先输出左子树、右子树，最后父节点

关键就是看父节点的输出顺序。

不论前序、中序、后序
每个节点会访问一次且仅访一次，所以复杂度线性于节点总数，所以是O(n)。