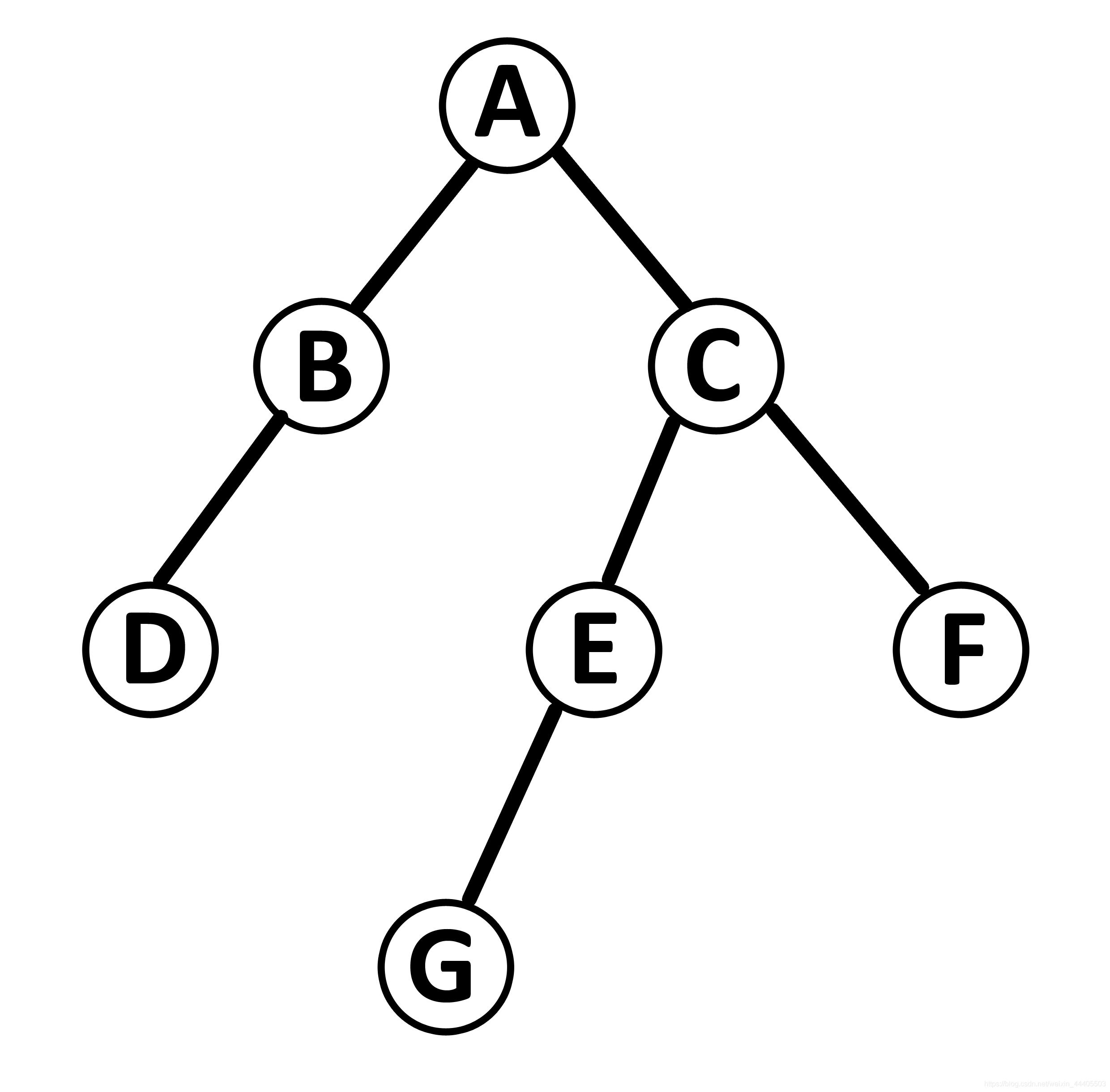
算法--树的定义
前言
树是一种逻辑上的概念,切记,这会帮助你理解。
学习算法过程中你不得立即获得正向反馈,这就是学习无奈的地方,学习更像是一种投资。
不要觉得学习带有功利性不好,努力考上一个好大学,找到好工作也是一种功利性,只是平时不愿意承认。
学习算法也是,你可以找到好工作,这是一种长期投资。
坚持下去。
树
树是一种逻辑上的概念,切记,这会帮助你理解。
树是一种数据结构
它是由n(n>=1)个有限结点组成一个具有层次关系的集合。
即最少一个节点。
树具有的特点有
- 每个结点有零个或多个子结点
- 没有父节点的结点称为根节点
- 每一个非根结点有且只有一个父节点
- 除了根结点外,每个子结点可以分为多个不相交的子树。
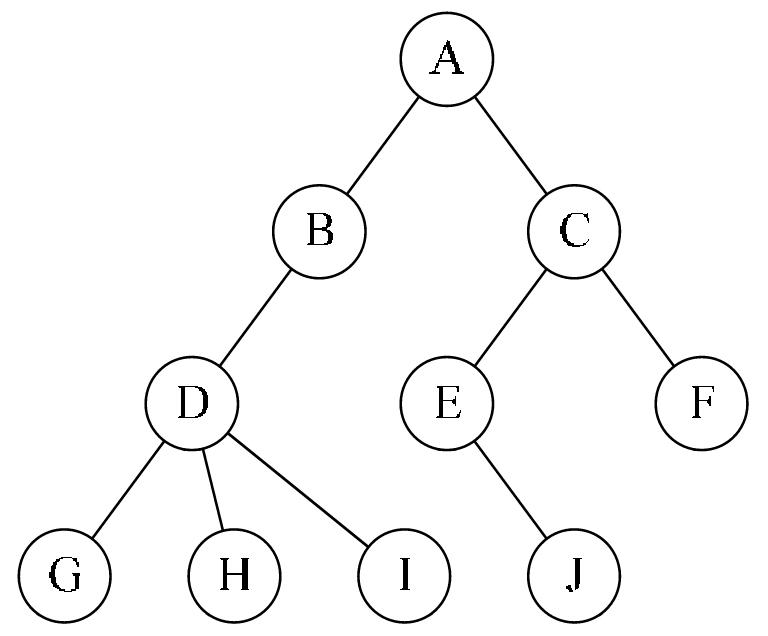
术语
- 结点的度(Degree):结点拥有的子树的数目,root,有 0-2个结点
- 叶子结点:度为0的结点 //就是最后一个节点
- 分支结点:度不为0的结点
- 树的度:树内各结点的度的最大的值。(即所有子节点加起来有多少度)
- 树的层次序号:每个节点,从上往下,从左往右都有一个编号,根是1,第二层最左是2依次递进
- 层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1
- 树的高度:树中结点的最大层次
- 森林:0个或多个不相交的树组成。
对森林加上一个根,森林即成为树;删去根,树即成为森林
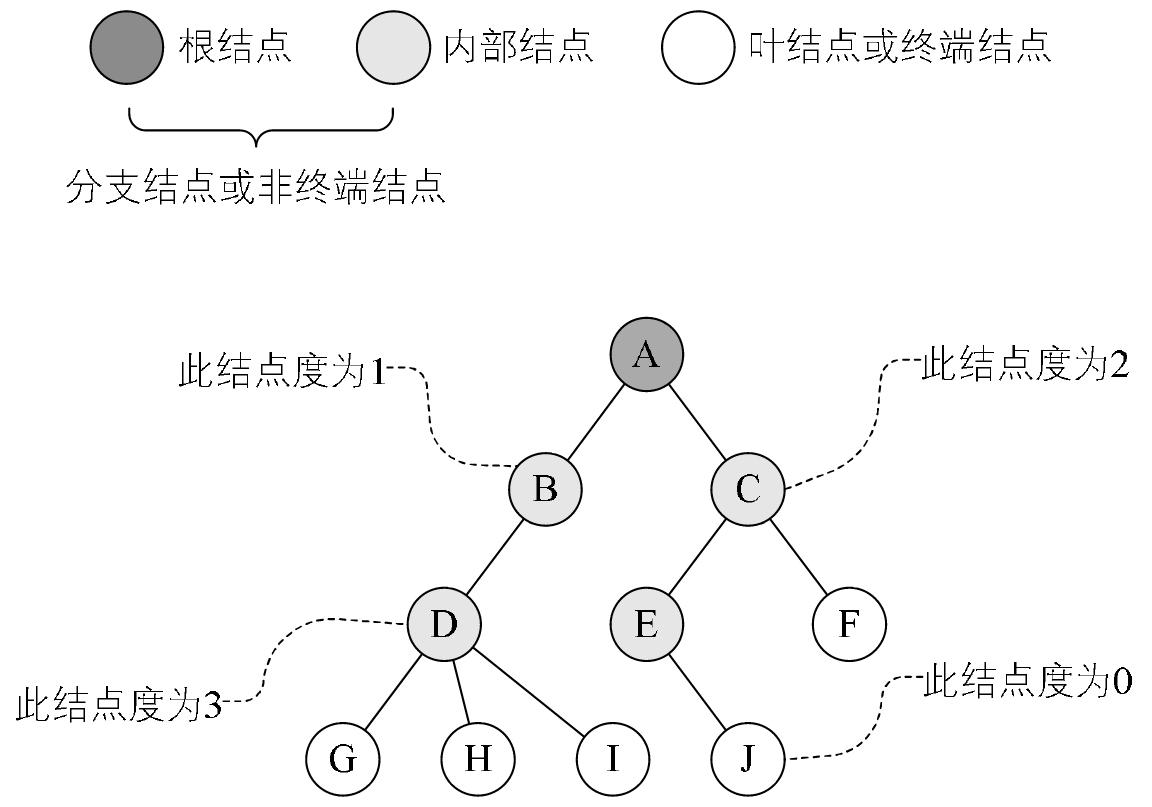
二叉树的度是指树中所以结点的度数的最大值。二叉树的度小于等于2,因为二叉树的定义要求二叉树中任意结点的度数(结点的分支数)小于等于2 。
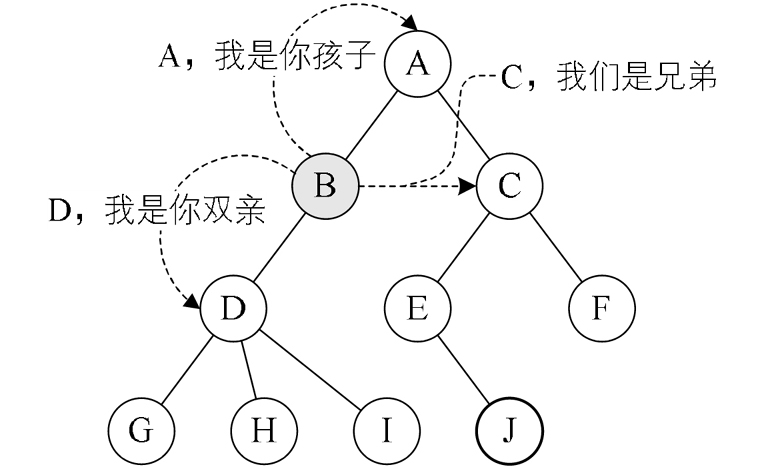
节点关系
若一个结点有子树,那么该结点称为子树根的"双亲",子树的根称为该结点的"孩子"。
有相同双亲的结点互为"兄弟"。
一个结点的所有子树上的任何结点都是该结点的后裔。
从根结点到某个结点的路径上的所有结点都是该结点的祖先。
节点的层次
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。
树中结点的最大层次称为树的深度(Depth)或高度。

总结
树是概念的结构,如果树只有一侧,也可以理解为一个链表,在逻辑上规定了树的结构。
概念性的东西,不容易记住,当可以记住时,可以当作字典来查询。
关键点在于,概念是用来帮助理解的,当你理解了之后,自然就可以记住概念。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 人话翻译机!
评论