树

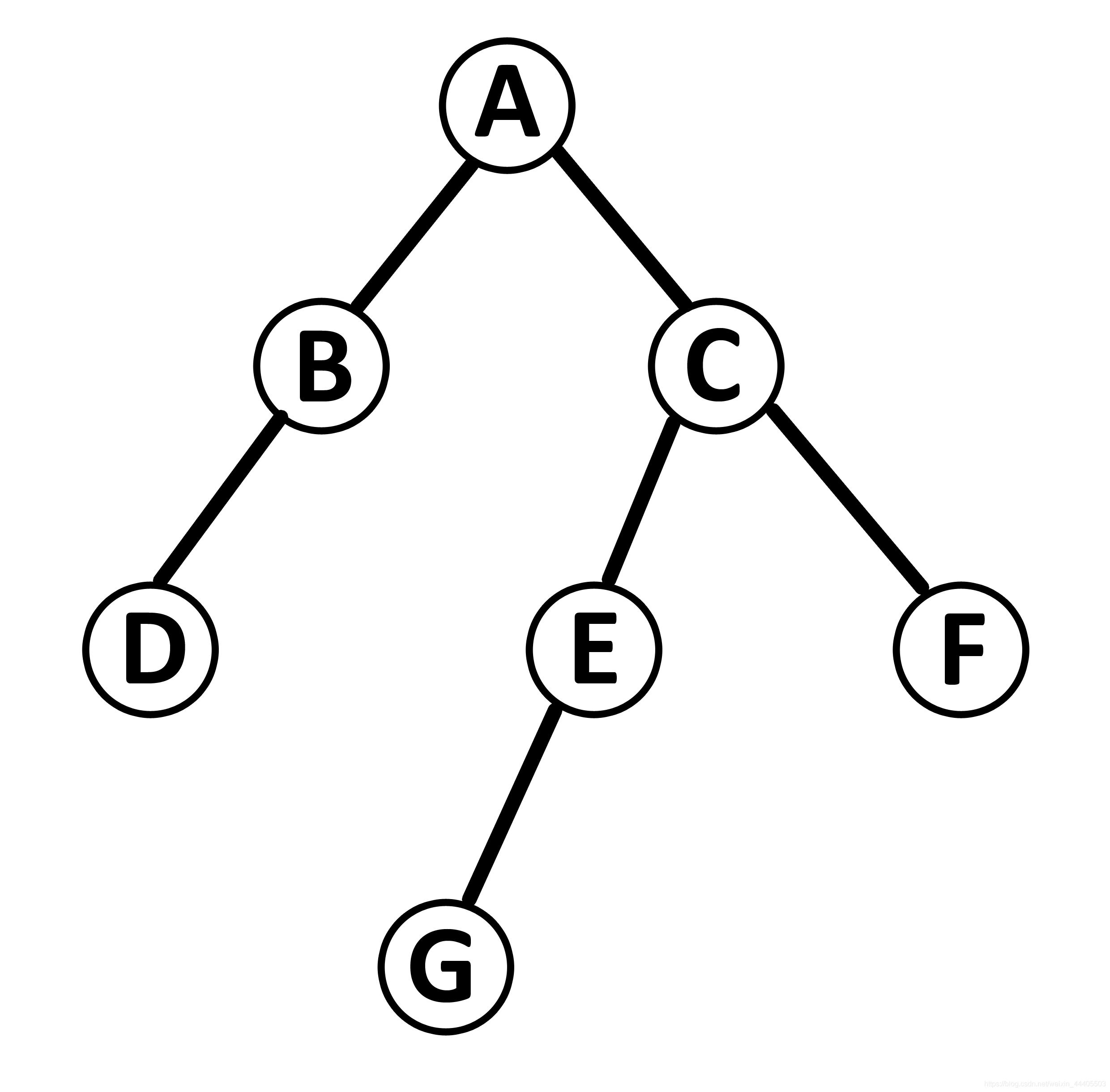
树即经典实用，又非常有助于学习算法。 前言二叉树是一个经典的数据结构，通过学习二叉树可以往后扩展学习更多类型的树。这里要强调几点： 树是逻辑上定义的数据结构，哪怕只有一个节点也可以称之为树。 不要慌，二叉树实际上比你想像的要容易上手。 这篇文章先讲概念，再讲实现。 二叉树二叉查找树也称为有序二叉查找树，满足二叉查找树的一般性质，是指一棵空树具有如下性质： 任意节点左子树不为空,则左子树的值均小于根节点的值； 任意节点右子树不为空,则右子树的值均大于于根节点的值； 任意节点的左右子树也分别是二叉查找树； 没有键值相等的节点； 不区分左右节点的值谁比谁大。叶子节点：没有子节点的节点。由于出版的问题，节点 和 结点 是一个意思。 二叉树五种状态树的五种状态要这样理解：为了抽象出树的各种情况下树当时的状态，而进行的命名。实际上就是当前树被操作当前状态。 空树: 就是null，一般是在操作中删完了。 单节点树：只有一个根结点的二叉树 只有左子树 只有右子树 满二叉树：每一次结构都达到最大值。就是完美状态总节点数=2^n-1，n 为层数。(等比数列求和) 完全二权树：叶子节点只能出 ...

前言 树是一种逻辑上的概念，切记，这会帮助你理解。 学习算法过程中你不得立即获得正向反馈，这就是学习无奈的地方，学习更像是一种投资。不要觉得学习带有功利性不好，努力考上一个好大学，找到好工作也是一种功利性，只是平时不愿意承认。学习算法也是，你可以找到好工作，这是一种长期投资。坚持下去。 树 树是一种逻辑上的概念，切记，这会帮助你理解。 树是一种数据结构它是由n（n>=1）个有限结点组成一个具有层次关系的集合。即最少一个节点。 树具有的特点有 每个结点有零个或多个子结点 没有父节点的结点称为根节点 每一个非根结点有且只有一个父节点 除了根结点外，每个子结点可以分为多个不相交的子树。 术语 结点的度(Degree)：结点拥有的子树的数目，root，有 0-2个结点 叶子结点：度为0的结点 //就是最后一个节点 分支结点：度不为0的结点 树的度：树内各结点的度的最大的值。（即所有子节点加起来有多少度） 树的层次序号：每个节点，从上往下，从左往右都有一个编号，根是1，第二层最左是2依次递进 层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1 树的 ...